Kohärenz
Die Wissenschaft ist der Versuch, die chaotische Mannigfaltigkeit unserer Sinneserfahrungen auf ein logisch einheitliches Gedankensystem zu bringen.
Albert Einstein, 1916
Synthalpie als Brücke zwischen Gravitation und Quantenmechanik
1. Einleitung
Die bisherigen physikalischen Grundtheorien, Allgemeine Relativitätstheorie (ART) und Quantenmechanik, beruhen auf unterschiedlichen Begriffsarchitekturen. Die ART beschreibt die Raumzeit als kontinuierliche Geometrie, deren Krümmung durch Energie und Impuls bestimmt wird. Die Quantenmechanik dagegen operiert mit diskreten Zuständen und Wahrscheinlichkeitsamplituden, die auf einer festen geometrischen Bühne definiert sind. Das Problem einer einheitlichen Theorie liegt darin, dass beide Ansätze inkommensurable Strukturen voraussetzen: Kontinuum und Diskretheit.
Das Konzept der Synthalpie bietet eine mögliche Lösung: Es beschreibt Systeme nicht über Substanz oder Ort, sondern über Kohärenz – das Maß, in dem Wechselwirkungen sich zu stabilen Beziehungen organisieren. Synthalpie fungiert damit als transversales Prinzip: sie gilt sowohl für physikalische als auch für soziale, biologische oder kognitive Systeme.
In physikalischer Formulierung lässt sie sich als Maß der lokalen Kohärenz zwischen Freiheitsgraden definieren. Damit entsteht ein Modell, das sowohl die Raumzeitstruktur als auch die Quantenkohärenz als Grenzfälle desselben Prozesses beschreibt.
2. Synthalpie als Funktional der Kohärenz
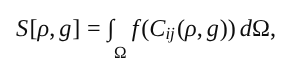
Formal kann Synthalpie als Funktional S über einem Zustandsfeld ρ und einer Metrik gμν eingeführt werden.
wobei Cij ein Korrelations- oder Informationsmaß zwischen den Komponenten i und j bezeichnet.
Je höher die interne Korrelation eines Systems, desto größer seine Synthalpie.
Die Dynamik ergibt sich aus der Variation von S unter Erhaltung der Normalisierung des Zustandsraums.
Wird der Gradient ∇S als treibende Kraft interpretiert, entstehen in unterschiedlichen Skalenbereichen verschiedene physikalische Erscheinungsformen:
– im makroskopischen Bereich geometrische Kohärenz (Gravitation),
– im mikroskopischen Bereich Zustandskohärenz (Quantenmechanik).
3. Gravitation als makroskopischer Synthalpiezustand
Auf der Skala makroskopischer Systeme führt die Maximierung der Synthalpie zur Stabilisierung von Raumzeitbeziehungen. Die resultierende Feldgleichung kann in der Form
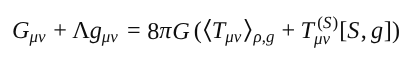
geschrieben werden.
Der zusätzliche Term Tμν(S) beschreibt die Kohärenzenergie des Feldes S und wird durch
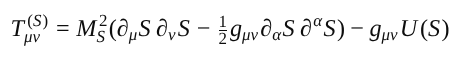
definiert.
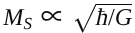
Damit koppelt Synthalpie direkt an die Planck-Skala.
Die Einstein-Gleichungen erscheinen damit als makroskopisches Gleichgewicht eines kohärenten Informationsflusses. Gravitation ist nicht eine zusätzliche Kraft, sondern der geometrische Ausdruck maximierter Kohärenz.
4. Quantenmechanik als mikroskopischer Synthalpieprozess
Auf der kleinsten Skala wird Synthalpie lokal als Fisher-Information wirksam.
Ein einfaches System lässt sich über Dichte ρ(x,t) und Phase ϕ(x,t) beschreiben.
Die zugehörige Synthalpie-Wirkung lautet:
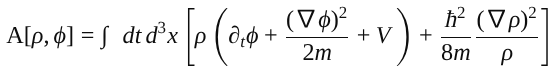
Die Variation dieser Wirkung liefert zwei gekoppelte Gleichungen:

Damit folgt die Quantenmechanik direkt aus der Variation eines Synthalpie-Funktionals, ohne zusätzliche Postulate.
5. Kohärenz als gemeinsamer Nenner
Vergleicht man beide Skalen, so entsteht eine formale Analogie:
| Ebene | dynamische Größe | Erscheinungsform der Synthalpie |
|---|---|---|
| Makroskopisch | gμν | Stabilisierung geometrischer Kohärenz (Gravitation) |
| Mikroskopisch | ψ | Erhaltung probabilistischer Kohärenz (Quantenmechanik) |
In beiden Fällen maximiert das System die lokale Kohärenz bei minimaler Entropieproduktion:
Die Gravitation stabilisiert die Kohärenz des Raumes, die Schrödingergleichung stabilisiert die Kohärenz des Zustands. Beide sind Ausdruck derselben Synthalpie auf verschiedenen Skalen.
6. Quantisierung als Grenzphänomen
Im Synthalpie-Modell tritt Quantisierung nicht als Axiom, sondern als Folge der Kohärenzsättigung auf.
Wenn die Kohärenz zwischen Freiheitsgraden nicht kontinuierlich aufrechterhalten werden kann, zerfällt sie in stabile diskrete Zustände.
Das Wirkungsquantum ℏ markiert die Grenze zwischen kontinuierlicher und diskreter Kohärenz.
Es erscheint nicht als willkürliche Konstante, sondern als Maß der minimalen Synthalpieeinheit:
ℏ ∼ ΔSminΔt
Damit wird deutlich: Raumzeitkontinuität (ART) und Zustandssuperposition (QM) sind keine Gegensätze,
sondern zwei kohärente Phasen desselben Prinzips.
7. Schlussfolgerung
Die Synthalpie-Theorie ersetzt das ontologische Dualismusproblem der modernen Physik durch ein einheitliches Organisationsprinzip.
Gravitation und Quantenmechanik erscheinen als Grenzfälle einer allgemeinen Dynamik der Kohärenz.
Mathematisch ergibt sich die Raumzeitkrümmung aus makroskopischer Synthalpie, die Schrödingergleichung aus mikroskopischer Synthalpie. Beide Ebenen werden über denselben Mechanismus verbunden: Maximierung von Kohärenz unter Nebenbedingungen der Energie und Information. Damit löst Synthalpie das Quantisierungsproblem nicht durch Vereinheitlichung zweier Theorien, sondern durch eine Neudefinition des Gemeinsamen. Was Gravitation krümmt und was Quanten interferieren lässt, ist ein und dieselbe Tendenz der Welt, Kohärenz zu erhalten.
Die Atome oder Elementarteilchen sind nicht real im Sinne von Dingen; sie bilden eine Welt von Möglichkeiten und nicht von Tatsachen.
Werner Heisenberg, 1969
